Q&A: Mathematical Vocabulary in Investigations 3

Question: How does Investigations approach the teaching and learning of mathematical vocabulary?

Answer: In Investigations 3, mathematical vocabulary is introduced as a natural part of the conversation during activities and discussions, along-side students’ own words. Rather than memorizing the definitions of new terms, students come to understand such words as factor or area or symmetry as they investigate and discuss new concepts. Hearing new mathematical terms used regularly, and having opportunities to use them in the context of activities and discussions, supports students in communicating their thinking clearly and in using increasingly precise mathematical language accurately.

Learning mathematical vocabulary is complex because a single word can encompass several ideas and relationships. Students in Investigations develop their understandings of mathematical terms as they progress through the grades. Take, for example, the term square. Work in the younger grades focuses on describing and identifying attributes of squares, constructing squares using different materials, and comparing squares to other 2-dimensional shapes. In the later grades, students revisit and refine their definition of a square as they examine attributes such as angle measurement and sets of parallel sides, and think about issues of classification such as whether a square is a rectangle and a rectangle a square. In this way, students’ knowledge of a term such as square develops with time and experience, within the context of their work with geometry and measurement.

The curriculum includes several features designed to support teachers in introducing and using accurate mathematical vocabulary with students. Mathematical terms related to the content being investigated are listed at the top of each session and are highlighted within the session. The blue Teacher Talk offers ways of introducing and using important vocabulary with students, while the Students Might Say feature provides teachers with a sense of what student language to expect during activities and discussions.

3U4 p. 132, 3U4 p. 134, & 3U4 p. 138

Differentiation suggestions located in the sessions provide information about providing vocabulary support to students who are learning English. (Additional information about previewing content for English Language Learners is included in the Differentiation Section at the front of each unit.)

3U4 p. 135

Located at the end of each unit, many Teacher Notes provide information about mathematical language. Dialogue Boxes—snippets of discussions based on actual student-teacher interactions— provide insight into how students communicate their mathematical thinking. These features are designed to support teachers as they work with their students to make sense of and use mathematical vocabulary.

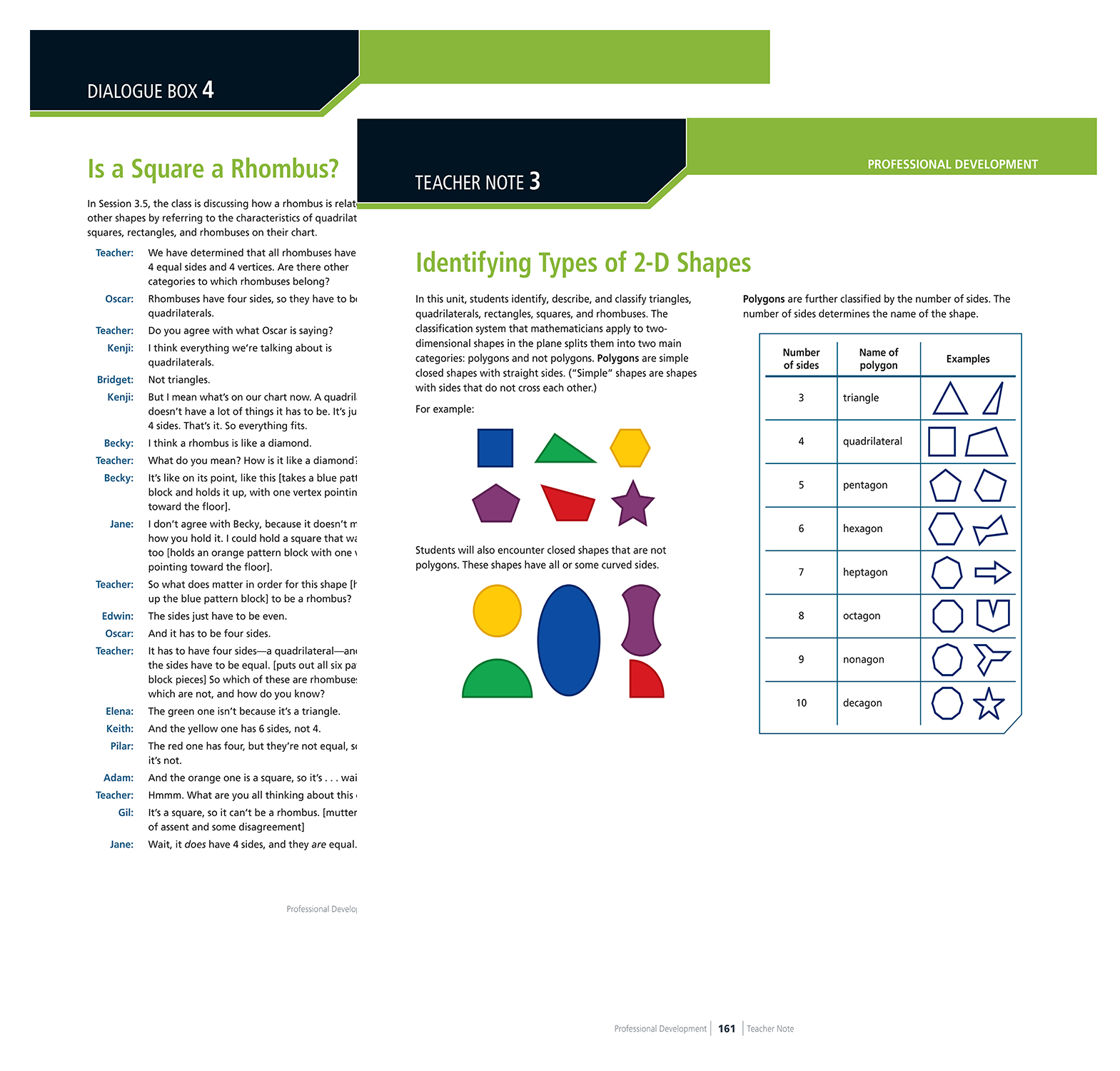
3U4 p. 172 & 3U4 p. 161

In some sessions, students generate grade-appropriate definitions for mathematical terms after they have had multiple opportunities to investigate and discuss the concept being defined. For example, at the end Session 1.2 of Unit 7 in second grade, students come together as a class to define even and odd numbers using their own language. As students engage, as a community, in writing a definition of even and odd numbers, they must work together to carefully select language that accurately conveys their understandings of even and odd numbers and explain why their claim is true for all numbers.

2U7 p. 36

In this way, creating more formal definitions of mathematical terms becomes a critical part of making sense of the mathematics (MP1), learning to communicate with precision (MP6), and even constructing arguments (MP3).

We are excited to have a space that offers us the opportunity to answer common questions from the field. Have questions you’d like to see answered? Email us.