In a blog post over a year ago, I wrote about the importance of using story contexts to support students in developing mental images of the operations. In that post, I concluded:
“Along with pictures, drawings, diagrams, equations, and physical models, story contexts are critical parts of a student’s repertoire of representations. In fact, it is often the case that three kinds of representations are in play: a numerical representation, a picture or diagram, and a story. Moving among these to see how each relates to the others is powerful in understanding the mathematical relationships in a problem.”
The purpose of making connections across these different kinds of representations is not only to find an answer to a single problem, or to use one representation to check another, but also to learn something general about how the arithmetic operation behaves. What connects these numbers, pictures or diagrams, and contexts is an underlying mathematical structure.
In the following example from a grade 3 class, the teacher is introducing a set of problems about multiplication and division by having students look at the first problem together (from Investigations 3, Grade 3, Unit 1, Investigation 4): A robot has 4 hands. Each hand has 6 fingers. How many fingers does the robot have altogether?
In a previous lesson, the class had talked about three quantities that are present in many multiplication situations: a number of groups (one of the factors), the number of things in each group (the other factor), and a total number of things (the product).
As you read this first part of the classroom dialogue, think about these questions: In what ways are students thinking just about this particular problem? In what ways are they considering something more general about the structure of the operation of multiplication, that is, the way multiplication behaves no matter what the numbers are?
Teacher: OK, what do we know here? Do we know the number of groups? Do we know the number in each group? Do we know our total? What do we think? What do we know?
Beatriz: Um, how many hands does each robot have.
Teacher: OK, so we know how many hands the robot has. So what is that? Is that the number of groups? Is that the number in each group? Picture a crazy robot with 4 hands on his body.
Kim: Um, the groups.
Teacher: Yeah, this right here is the number of groups. So we know that a robot has 4 hands so we’re going to call that 4 groups. The other piece of information we know is that each hand has 6 fingers. So is that our total answer or is that the number in each group?
Arthur: That’s the number in each group.
Teacher: So, what’s missing? … Benjamin?
Benjamin: I’m just trying to say the times table but…
Teacher: So you think that this is like a times table problem, a multiplication problem? [Benjamin nods.]
Philip: It’s like, he has, like the robot has 4 hands and you gotta count 6, you gotta count 4 times, you gotta count 4 times with 6 fingers.
Teacher: OK, so that’s a good way to describe how you know it’s a multiplication problem. What would be an equation for this one?
Oscar: 4 times 6 equals something.
Teacher: And if we were to label our final answer? What would that label be? What are we trying to find out?
Beatriz: Robot fingers.
Teacher: Robot fingers. So whatever our answer is, it’s the total of robot fingers.
The teacher encourages students to use the language of “groups” and takes advantage of Philip’s description of counting by equal groups—“you gotta count 4 times with 6 fingers”—to emphasize how that characterizes the operation of multiplication. In classroom work, we find that, without this kind of focus on structure, many students don’t see how the three quantities are related and can’t answer the question, “where do you see multiplication in this problem?” For example, in a research project about mathematical argument, many students who could solve a multiplication problem like 4 × 6 were nevertheless unable to write a story problem that represented that expression. They could perform the computation but were not visualizing how it represented multiplication.
After the discussion of this first problem, the teacher is ready to send students back to their seats to work on the problem set. But students are still having other thoughts they want to share. The teacher pauses because she sees that students are eager to articulate their ideas. Denzel says, “This reminds me when we was counting around the room by 6,” and Ines responds, “I was thinking you could count by 4’s too.” Denzel is noticing the structural similarity between solving the robot fingers problem and a previous activity, Counting Around the Class; Ines is implicitly calling on the commutative property of multiplication. Then Oscar raises his hand.

Oscar: 4 times 6 is like another doubling idea.
Teacher: What do you mean?
Oscar: Because if you take, if you break 4 into two and two, then you can do two 6’s equals 12 and another two 6’s equals 12.
Teacher: So I hear you breaking that 4 × 6 down into two smaller facts to help you. And if I remember correctly, you actually brought that up when we looked at a 4 by 6 array last week. Oscar was one of the first ones to say how we could look at the 2 times 6 because he knew the two 6’s made a 12. [She draws a quick diagram.]
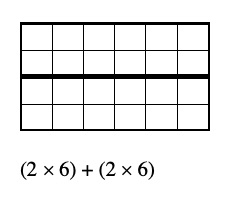
Teacher: So Oscar is thinking about a 2 times 6 and adding it to another 2 times 6. That whole doubling idea. So that might be something to think about, too.
When Oscar says “4 × 6 is like another doubling idea,” he refers to a structure that he has seen occur before—dividing one factor of a multiplication expression (4 × 6) in half to get a new expression (2 × 6), solving the new expression, then doubling its product. Underlying Oscar’s remarks is an idea related to the distributive property of multiplication over addition:
4 × 6 = (2 + 2) × 6 = (2 × 6) + (2 × 6).
These students are “lifting off” from the particular problem and thinking about multiplicative structure as they move back and forth among models and pictures, story contexts, and numbers and symbols. The teacher supports those ideas: this is a classroom in which students understand that such connections, not just single answers to problems, are encouraged and respected. If students are expected to focus not only on individual numerical answers to individual problems but also on the structure of the operations, they are oriented differently: they notice patterns, regularities, and relationships that are critical for building a strong foundation of meaning for the operations.
- Robot Fingers and Multiplicative Structure - March 9, 2020
- The Bad Rep of Word Problems: “Two trains leave the station…” - October 22, 2018
- Asked and Answered: Why Ask the Same Question When You’ve Already Gotten a Perfectly Good Answer? - January 26, 2018

