Take a moment, before looking at the student work and video below. How would you use your fingers to solve a problem about having 12 scissors, and lending 5 to another class?
A student I’ll call Miguel is a first grader, in a class that has been working on solving addition and subtraction story problems and recording their solution strategies. Here is a basic recreation of Miguel’s written work for the scissors problem.
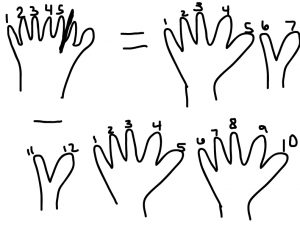
A (basic) recreation of Miguel’s written work
![]() What do you notice about Miguel’s work? How do you think he solved the problem? Given this work, what would you ask him?
What do you notice about Miguel’s work? How do you think he solved the problem? Given this work, what would you ask him?
Luckily, we know and can reflect on what Miguel’s teacher asked:
![]() Now how do you think Miguel solved the problem? Did he demonstrate any knowledge in his explanation that wasn’t evident in his written work?
Now how do you think Miguel solved the problem? Did he demonstrate any knowledge in his explanation that wasn’t evident in his written work?
Miguel’s paper shows 12 fingers, a minus sign, 5 fingers, an equal sign, and 7 fingers, but it does not show how he knows that 12 minus 5 equals 7. The teacher describes what she sees (12 fingers and 5 fingers) and asks, after gesturing over the 7 fingers, “But how do you know that that equaled 7? What did you do with your fingers? Or what did you think in your mind?” Knowing that showing one’s thinking on paper is challenging for first graders — particularly for subtraction and for strategies that involve fingers — the teacher asks Miguel to show how he used his fingers.
I’ve watched this video many, many times, and I find how Miguel actually used his fingers fascinating every single time. He knows that two hands make 10 fingers, and that he needs 10 fingers and 2 more to show 12. Since he cannot show 12 fingers he has to imagine 5 and 5 and 2 while showing either 5 and 5, or 5 and 2 fingers. He closes one open hand to represent removing 5, and almost instantly displays the 2 additional fingers that he was mentally holding onto. He is left with 5 and 2 more. Which makes 7. Whew. (This is my interpretation. Do you agree? Go back and watch it again.)
While many think of 12-5 as a simple problem, this clip shows the work of making sense of – and helping students make sense of – subtraction in the primary grades. Think about how hard Miguel worked to model and articulate his strategy. Now imagine trying to show that strategy on paper. One next step is helping Miguel find ways to record in a way that more accurately reflects his strategy. For example, he might cross out the 5 fingers he removed in his initial drawing of 12, and then renumber the fingers that are left.
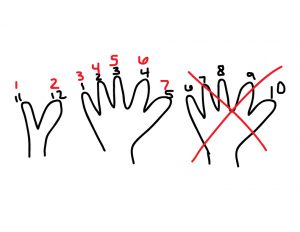
One possible recording method for Miguel’s strategy
Work relating the quantities and actions in different stories to numbers and symbols and to a variety of representations will also help Miguel come to see how equations like 12 – 5 = 7 can represent his work.
As always, there are next steps. At the end of the day, though, I’m left – as I often am – thinking about the complexity of the operation of subtraction, and the mathematical thinking that students bring to it. And how it never ceases to amaze me what can happen when we trust students to solve problems in ways that makes sense to them.
- Developing Classroom Agreements in the Investigations 3 Classroom - October 25, 2021
- Meaningful Math Discussions: It’s about the Ideas, Not Where You Discuss Them - April 12, 2021
- Teaching Investigations 3 Remotely: Not So Different - February 22, 2021


Very interesting post Megan! Reminds me a of an interesting story that happened on a project I worked on a few years ago. The student called them invisible fingers and we wrote the story up here. https://www.teachingisproblemsolving.org/whats-next-stories/lilys-invisible-fingers/
Although, I think Miguel’s strategy is very complex and I think your interpretation is correct. Fascinating stuff!
Thanks Zak, I’ve never been able to get enough of this clip! Your story about the “invisible fingers” strategy raises something I’ve always wondered about Miguel’s – what would he have done if the problem wasn’t about subtracting 5, which can be easily represented by removing one whole hand (rather than thinking about it as minus 2, minus 3). Thanks for sharing the link.
Yeah – I wish we could go back and time and change the story to subtracting six or subtracting three to see what Miguel may do with that problem. I think both would be fascinating! -Zak
I really like this as an example of the student working on the subject and the teacher working on the student.
I’m a retired Silent Way teacher of English as a foreign language. I find lots of similitudes between teaching languages and teaching maths
“The student working on the subject and the teacher working on the student” is an interesting way to put it! Your second comment makes me think of an ESL teacher who once told me how – as she changed the way she taught math – mathematics had become such a rich/valuable venue for her work on language. Thanks for reading and commenting Glenys.
I didn’t invent the phrase “The student working on the subject and the teacher working on the student”. It’s a clarification of what Caleb Gattegno meant by the pedagogy of subordinating teaching to learning: http://subtle.site/
I too learnt a lot by attending maths training sessions. It seems to me many more maths teachers than language teachers put this approach into practice in their classrooms even if they’ve never heard of Gattegno.
Great video and blog! Thanks for posting. He’s internalized the tool and made a mental image – how cool! This is a goal we want for our students, right? It also makes me wonder if perhaps the numbers lend themselves to this tool/strategy for Miguel. He seems to use 10 as a landmark and adjust at the end. 10-5=5 and now to account for that extra 2 I have, pretty sophisticated! Curious about what he does with other problems.
Thanks for reading and commenting Deepa! Yes, it’s exciting when a physical tool becomes a mental model they can use. And Zak and I were wondering the same thing – what would Miguel have done if it was 12-3 or 12-6? Subtracting 5 is handy (ha!) when you’re modeling with fingers. Would he shift to subtracting to get to 10, and then subtracting the rest (e.g. 12-2-1, 12-2-4)? Would love to know.