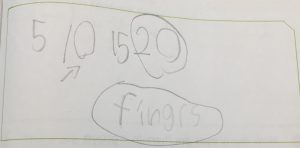The Hard Work of Counting by Groups

The other day I visited a class that was at the very beginning of How Many Tens? How Many Ones?, the final unit of the grade 1 sequence on Addition, Subtraction and the Number System. The class began with a conversation in which they modeled, recorded, and discussed the previous day’s work, about the number of hands on different numbers of people, organized as a table. The teacher then explained that today they were going to be thinking about fingers instead of hands. With minimal introduction, students set to work on two problems.

1)    How many fingers on 4 hands?

2)    How many fingers on 8 hands?

As I wandered, I saw lots of strategies for accurately solving these problems. I saw pictures of hands and pictures of people, with fingers counted by 1s, 5s, and 10s, and I saw numbers (e.g. 5s or 10s), expressions, and equations (e.g. 10+10=20 and 5+5+5+5=20).

I also had a few really interesting conversations that reminded me how challenging it is to shift from thinking about 1s to thinking about groups. (Note: All student names are pseudonyms.)

Count by 2s

When I arrived at Vera’s desk she was hard at work, figuring out the number of fingers on 8 hands. She had carefully drawn 8 hands. When I asked, she told me, “I’m counting them by 2s.” (Remember: yesterday, and at the start of class, they were focused on people and hands.)

Vera was very careful and precise, and persevered until the last finger was labeled 80. Like a colleague of mine has been known to say, she found the answer to a different question. (Can you think of what that question would be?? e.g. how many hands on 40 people?)

This is a strategy that’s not unusual to see as students shift from thinking about and counting by 1s to thinking about and counting by groups. Vera knows the class is in new territory and is challenging herself to count by groups. She knows the rote sequence. (And she knows counting by 2s has recently been the focus of math class, when the class solved problems about hands and people.) However, she is not yet connecting that sequence to quantities; that each number refers to a group of 2 things. Luckily, this is the focus of the rest of the Unit.

Count by 5s, Count by 8s

When I joined Evan, he had already written 5+5+5+5=20 beneath the question about how many fingers there are on 4 hands. I asked how he thought about the problem.

Evan: I did 5+5+5+5.

“Why did you add four 5s? … (He is quiet.) … What does this 5 (pointing to the first 5 in his equation) represent? What does it stand for in the problem (pointing back to the text of the problem)?”

Evan: That’s the fingers on one hand.

We talked through the other 5s and then I asked how he knew the answer was 20.

Evan: I went like this.

He placed the tip of his pencil under the first 5 and touched it down as he counted: “1, 2, 3, 4, 5.” He moved his pencil to the second 5: “6, 7, 8, 9, 10.” And did the same for the next two 5s, reaching a total of 20.

For the problem about how many fingers on 8 hands, he had written 8 + 8 + 8 + 8 + 8 + 8 +8 + 8. “I see that now you’re working on the problem about how many fingers are on 8 hands. Can you tell me what you’re thinking?”

Evan: I did the same thing. 8 + 8 … + 8. Now I have to figure out what that is.

I pointed to the first 8 in his equation. “I’m going to ask the same question as before. What does this 8 represent?”

Evan studied the problem. … “Oops! They should be 5s.”

He erased the 8s, and started changing them to 5s. When I checked his workbook later, he ended up with seven 5s instead of eight, and a total of 34 fingers.

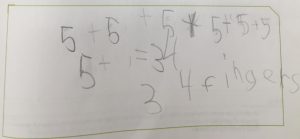
My first surprise was that a student that knew he could write 5+5+5+5 to represent this problem counted by 1s to solve it. I was not surprised at the switch to adding 8s. Keeping track of what the numbers in a problem like this mean is the work — Which is the number of groups? Which is the number in each group? What happens when you reverse them? I was happy to see him quickly discover his error when directed back to the context. I wonder if, after the discussion and the making of a table of hands/fingers, 34 would “sound funny” to Evan as an answer to this problem. I wish I had had the chance to ask him!

Fingers on People Instead of Fingers on Hands

When I joined Leigh, she was finishing up her work on the problem about fingers on 4 hands. She told me, “It’s 40.”  I asked how she figured it out.

Leigh: I know one person has 10 fingers. So 10, 20, 30, 40.

I asked her to reread the problem. She did, accurately, and looked at me. “10, 20, 30, 40.”

She didn’t say “duh” but she might as well have! I saw a handful of students who interpreted the problem as how many fingers on 4 people instead of 4 hands.

Raha’s work

As much as it might seem (and might be) a question of reading comprehension, I think we underestimate the challenge that comes with problems that involve multiple units. While fingers are a useful context because we have them and they are great for modeling such problems, they are also connected to several different units: people (1s), hands (2s), fingers (5s or 10s). They can be counted by 1s, by 5s, or by 10s. You can think about this problem in tens (10 + 10 represents two pairs of hands), but 4 tens do not accurately represent the problem. This is not inconsequential work for 6- and 7-year olds.

As a final note, the teacher also noticed that several children found the number of fingers on 4 people instead of hands, and made sure it came up in the conversation at the end of class. After discussing several strategies that resulted in an answer of 20, she asked Tom to share the conversation they had had. He said, “Well I was thinking about PEOPLE.” Megan chimed in, “Me too, I was too! I got 40 b/c 10, 20, 30, 40.” The teacher asked students to model and count fingers on 4 people, and then asked what they’d have to do to model fingers on 4 hands. Jillian said, “We need only 4 hands. 2 kids have to sit down.” They counted the fingers and there seemed to be agreement that there are 20 fingers on 4 hands.

The complexity of the work of counting, and counting by groups, never ceases to amaze me. We spend much of Kindergarten and Grade 1 working with students to accurately count a set of objects by ones. Our goals? We want students to count each item once and only once; to say one number for each object; to move or keep track of each object as it is counted. The shift to counting by groups changes those goals. Problems about hands and fingers can involve groups of 2, 5, or 10, each with their own challenges. The work continues to be determining what it is that’s being counted, making decisions about how to count it, and figuring out how to keep track of that count. In fact, this is a thread across the elementary grades and can be seen in several of our previous blogs: And Then, She Waited, That Seems Way Too Big!, and Counting is Serious Business.